POWRÓT DO ARTYKUŁÓW

Analiza ryzyka w rachunku opłacalności inwestycji

(Dane liczbowe zaprezentowane w poniższym przykładzie są całkowicie fikcyjne. Zostały one przeze mnie wymyślone dla potrzeb niniejszego artykułu).

Dynamika zmian otoczenia, w którym działają przedsiębiorstwa w dzisiejszych czasach, a także rosnąca konkurencja powodują konieczność ciągłego rozwoju firm. Ma to na celu uzyskanie przewagi w stosunku do innych podmiotów rynkowych. Wzrost konkurencyjności to zasadniczy cel podejmowanych przez przedsiębiorstwa strategii działania. Strategiom tym nieodłącznie towarzyszą inwestycje. Są one koniecznością, jednak spełniają swoją funkcję tylko wtedy, gdy są efektywne. Jest bardzo dużo metod i narzędzi pozwalających ocenić opłacalność projektu inwestycyjnego. Metody te są powszechnie stosowane przez przedsiębiorstwa przygotowujące się do realizacji inwestycji, a także przez banki udzielające kredytów inwestycyjnych. Właściwie przygotowane projekcje finansowe, uwzględniające przepływy pieniężne netto mają zasadnicze znaczenie przy badaniu opłacalności inwestycji. Jednak inwestowanie nieodłącznie wiąże się z ryzykiem. Ograniczanie się przy badaniu opłacalności projektów inwestycyjnych jedynie do metod prostych lub dyskontowych (NPV, IRR) bez analizy ryzyka nie daje pełnego obrazu sytuacji. Może się bowiem zdarzyć, że projekt inwestycyjny wydaje się bardzo atrakcyjny. Jednak ryzyko mu towarzyszące jest na tyle duże, że niewielu inwestorów zdecydowałoby się na jego realizację. Wskazuje to na konieczność uwzględniania ryzyka w rachunku opłacalności projektu inwestycyjnego. Jak już wcześniej wspomniałem, metody badania opłacalności inwestycji są powszechnie stosowane w licznych przedsiębiorstwach. Jednak jeśli chodzi o analizę ryzyka, sytuacja jest o wiele gorsza. Metody uwzględniania ryzyka w rachunku opłacalności inwestycji są czasami pomijane, co może świadczyć o nieświadomości decydentów lub ignorowaniu ryzyka. Dlatego celem niniejszego artykułu jest przybliżenie tematyki ryzyka towarzyszącego inwestycjom oraz wskazanie metod mierzenia i analizowania tego ryzyka.

Spójrzmy na przykład firmy transportowej, która zamierza uruchomić połączenia autobusowe między dwoma miastami. Spółka rozpatruje trzy warianty realizacji inwestycji:

- zakup własny środków transportu,

- kredytowanie,

- leasing operacyjny.

Już na etapie kalkulacji opłacalności każdego z wariantów należy tak określić stopę dyskonta, aby uwzględniała ryzyko danej inwestycji. Wyższe ryzyko może być zaakceptowane pod warunkiem odpowiedniej premii za ryzyko. Jeżeli podstawową metodą oceny projektu jest NPV, to spełnienie oczekiwań inwestorów oznacza konieczność zwiększenia stopy dyskonta. Zastosowanie wyższej stopy dyskonta powoduje spadek wartości NPV, przy czym kryterium oceny nie zmienia się, tzn. gdy NPV >= 0, projekt należy zaakceptować. W praktyce jako stopa dyskonta najczęściej jest stosowany średni ważony koszt kapitału WACC. Natomiast stopa dyskonta uwzględniająca ryzyko to odpowiednio skorygowana wartość WACC. Jeżeli ryzyko projektu jest wyższe niż przeciętne, to wartość WACC jest zwiększana, aby zrekompensować dodatkowe ryzyko. Wysokość premii za ryzyko zależy od wielkości tego ryzyka i stosunku decydenta do ryzyka i jest ustalana indywidualnie. W praktyce są stosowane na ogół dwa rozwiązania w tym zakresie:

- rozwiązanie subiektywne,

- rozwiązanie obiektywne (współczynnik zmienności) - podejście probabilistyczne oparte na wartości oczekiwanej i odchyleniu standardowym.

W analizowanej firmie przy obliczeniu NPV stopa dyskontowa została skorygowana o premię ryzyka wynoszącą 5%. Wartość ta wynikała z rozmiaru ryzyka związanego z realizacją danego projektu. Dla poszczególnych wariantów inwestycji NPV wyniosło:

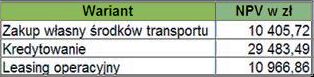
Pierwsze spojrzenie na powyższe dane sugeruje, że wszystkie warianty powinny przynieść stopę zwrotu wyższą od granicznej. Opierając się na NPV, za najbardziej opłacalny należało uznać wariant kredytowania. Najniższa wartość NPV występowała w przypadku zakupu własnego. Jednak, aby dokładniej przeanalizować wszystkie warianty, należy uwzględnić w rachunku opłacalności ryzyko. Zdarzają się bowiem sytuacje, że warianty najbardziej opłacalne z punktu widzenia NPV charakteryzują się również najwyższym ryzykiem. Analiza ryzyka projektów inwestycyjnych jest zatem niezbędna do określenia atrakcyjności poszczególnych wariantów realizacji inwestycji.

Aby dokładniej poznać projekt i jego efekty sporządzono zatem analizę scenariuszy, dzięki czemu zidentyfikowano różne możliwe sytuacje w przyszłości, a także lepiej oszacowano czynniki wpływające na wartość NPV. Poniżej pokazano wartości NPV dla trzech scenariuszy kształtowania się sytuacji.

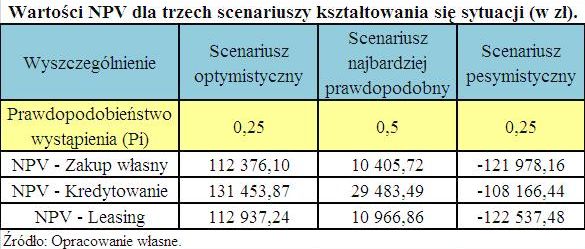
Scenariusz optymistyczny zakłada wzrost liczby przewożonych pasażerów podczas jednego kursu. Ponadto zakłada się tutaj spadek kosztów serwisów i napraw o 10% w porównaniu z wariantem najbardziej prawdopodobnym. W przypadku scenariusza pesymistycznego założono spadek liczby przewożonych pasażerów przy jednoczesnym wzroście kosztów paliwa o 10%, pozostałych kosztów o 5% oraz usług obcych o 5% w porównaniu z wariantem najbardziej prawdopodobnym. Jak wynika z powyższej tabeli w przypadku zaistnienia scenariusza pesymistycznego, żaden z analizowanych projektów nie byłby opłacalny. Informacje uzyskane dzięki analizie scenariuszy wykorzystano do obliczenia wartości oczekiwanej NPV oraz odchylenia standardowego NPV. Dzięki temu uzyskano odpowiednie informacje, przydatne przy podejmowaniu decyzji inwestycyjnych.

E(NPV) zakup własny = 112 376,10*0,25 + 10 405,72*0,5 - 121 978,16*0,25 = 2 802,35 zł.

E(NPV) kredyt = 131 453,87*0,25 + 29 483,49*0,5 - 108 166,44*0,25 = 20 563,60 zł.

E(NPV) leasing = 112 937,24*0,25 + 10 966,86*0,5 - 122 537,48*0,25 = 3 083,37 zł.

S(NPV) zakup własny = 83 204,87 zł.

S(NPV) kredyt = 85 186,86 zł.

S(NPV) leasing = 83 625,31 zł.

Z powyższych obliczeń wynika, że najwyższą wartością oczekiwaną NPV charakteryzuje się wariant inwestycji związany z kredytowaniem. Podobnie jak przy wyliczeniach NPV dla wariantu najbardziej prawdopodobnego, najniższe wartości związane są z wariantem zakupu własnego. Jednak kredytowanie charakteryzuje się najwyższą wartością miary ryzyka, jaką jest odchylenie standardowe. Sytuacja taka wymaga obliczenia współczynnika zmienności, który jednoznacznie wskaże najlepszy wariant z punktu widzenia opłacalności i ryzyka.

Współczynnik zmienności (zakup własny) = 29,69

Współczynnik zmienności ( kredyt) = 4,14

Współczynnik zmienności ( leasing) = 27,12

Powyższe obliczenia wskazują wariant kredytowania jako najlepszy. Jednak współczynnik zmienności dla tego wariantu jest dość wysoki. Niektórzy autorzy już dla współczynnika wynoszącego 0,5 zalecają skorygowanie stopy procentowej o premię ryzyka wynoszącą 3 punkty procentowe. Współczynnik zmienności na poziomie 4,14 może świadczyć o dużym ryzyku towarzyszącym analizowanej inwestycji. Powyższa metoda, poza wyliczeniem NPV opartym na wartościach oczekiwanych wpływów i wydatków wariantu najbardziej prawdopodobnego, dokonuje analizy projektu bazując na założeniu, że sytuacja ułoży się dla niego we wszystkich aspektach bardzo niekorzystnie lub też bardzo korzystnie.

Istotną wadą tej techniki jest jednak to, że uwzględnia ona jedynie trzy sytuacje: najbardziej prawdopodobną, najlepszą oraz najgorszą. Prawdopodobieństwo, że wszystkie aspekty projektu przyjmą jednocześnie ekstremalne wartości (najlepsze lub najgorsze) nie jest jednak zazwyczaj duże. W rzeczywistości NPV przybierać może nie tylko trzy możliwe stany, ale znacznie więcej. Ten aspekt ryzyka może być zbadany przez zastosowanie modelu symulacyjnego. Zakłada się tutaj, że NPV projektu może przybrać nieskończoną ilość wariantów. Rzeczywiście osiągnięty poziom NPV najczęściej może koncentrować się wokół wartości oczekiwanej NPV w taki sposób, że jego rozkład prawdopodobieństwa może być traktowany jako rozkład normalny mający kształt krzywej Gaussa, której kształt wyznacza średnia (wartość oczekiwana) oraz odchylenie standardowe.

Rozkład normalny jest symetryczny, co ma duże znaczenie, ponieważ znany jest procent wszystkich możliwych wartości zmiennych leżących w oddaleniu od wartości oczekiwanej, nie przekraczających określonej wielokrotności odchylenia standardowego.

Na podstawie znajomości rozkładu normalnego można określić prawdopodobieństwo, że NPV znajdzie się w określonym przedziale wartości. Np. 68,27% wszystkich możliwych wartości leży w przedziale [E(NPV) - 1S; E(NPV) + 1S].

Jeśli więc dla wariantu kredytowania E(NPV) = 20 563,60, a odchylenie standardowe 85 186,86, to 68,27% wszystkich możliwych wartości NPV leży w przedziale: [-64 623,26; 105 750,46].

Bardzo ważną informacją jest określenie prawdopodobieństwa zaistnienia zdarzenia, polegającego na tym, że NPV inwestycji będzie wynosiła określoną wartość (np. będzie mniejsza od zera, a więc prawdopodobieństwo tego, że projekt okaże się nieopłacalny dla inwestora). W tym przypadku stosowana jest forma zestandaryzowanego rozkładu normalnego, dla którego za pomocą standaryzacji szacowana jest nowa wartość zmiennej Z.

Z = [NPV - E(NPV)]/S

Zmienna zestandaryzowana Z ma rozkład normalny o E(NPV) = 0 i S(NPV) = 1. Tablice obszarów pod krzywą standaryzowanego rozkładu normalnego są publikowane, w związku z czym powierzchnię pod dowolną krzywą normalną można znaleźć przekształcając wartość zmiennej w wartość zestandaryzowaną Z i posługując się tablicami statystycznymi rozkładu normalnego. Wartość Z informuje o ile odchyleń standardowych założona przez nas wartość jest odległa od wartości oczekiwanej NPV.

Z (wariant kredytowania) = (0 - 20 563,60)/85 186,86 = - 0,241

W naszym przypadku odległość ta wynosi -0,241, co oznacza, że NPV wynoszące zero leży na wykresie po lewej stronie od wartości oczekiwanej NPV. Dla Z = 0,241 odpowiadająca mu wartość prawdopodobieństwa wynosi ok. 0,40. Tak więc prawdopodobieństwo, że dla danego projektu NPV < 0 wynosi 40%, zaś prawdopodobieństwo, że NPV > 0 wynosi 1 - 0,40 tzn. 60%.

Powyższe obliczenia świadczą o dość wysokim ryzyku towarzyszącym realizacji analizowanego projektu inwestycyjnego. Do dalszych rozważań przyjęto jedynie wariant polegający na zaciągnięciu kredytu w banku. Jest on najbardziej opłacalny dla inwestora i charakteryzuje się najmniejszym ryzykiem w porównaniu z innymi wariantami. Jednak uzyskanie kredytu wiąże się z licznymi warunkami. Bank musi uzyskać satysfakcjonujące zabezpieczenia. Ponadto cena kredytu musi uwzględniać ryzyko banku.

Analiza scenariuszy i analiza symulacyjna pozwoliły określić ryzyko towarzyszące danemu projektowi inwestycyjnemu. Jest ono stosunkowo duże. Prawdopodobieństwo, że projekt będzie opłacalny dla wariantu kredytowania wynosi jedynie 60%. Podjęcie decyzji o realizacji inwestycji zależy zatem od indywidualnego stosunku inwestorów do ryzyka. Pomocna w tym zakresie może być analiza wrażliwości, która wskaże elementy, na które najbardziej narażona jest wartość NPV i które należałoby szczególnie monitorować w przypadku podjęcia decyzji o realizacji inwestycji.

Badanie wrażliwości NPV przeprowadzono zakładając zmianę następujących parametrów wejściowych:

- spadek sprzedaży o 5 oraz 10%,

- wzrost kosztów paliwa o 5 oraz 10%.

Wartości NPV dla analizy wrażliwości przedstawiono w poniższej tabeli.

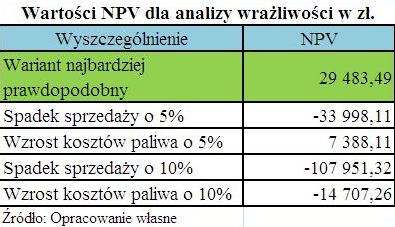
Analizując otrzymane wyniki można stwierdzić, że badany projekt jest najbardziej wrażliwy na zmiany sprzedaży. Spadek sprzedaży o 5% powoduje, że przy założonej stopie dyskonta projekt staje się nieopłacalny. Wzrost kosztów paliwa o 5% ma wpływ na obniżenie wartości NPV, jednak jest ona jeszcze dodatnia. Dopuszczalna zmiana przychodów ze sprzedaży, zapewniająca opłacalność inwestycji to 2,2%. Natomiast koszty paliwa mogą maksymalnie wzrosnąć o 6,67%. Ważną informacją dla inwestora, wynikającą z analizy wrażliwości jest to, że w przypadku akceptacji projektu należy zwrócić szczególną wagę na wielkość sprzedaży. W wariancie najbardziej prawdopodobnym założono 72,22 - procentowe wykorzystanie posiadanego taboru autobusowego przez pasażerów. Jest to ostrożne założenie. Nie zmienia to jednak faktu, że przy 10 procentowym spadku sprzedaży projekt będzie nieopłacalny. Dana inwestycja jest bowiem bardzo wrażliwa na przychody ze sprzedaży. Należy zatem, w przypadku akceptacji projektu ściśle monitorować sprzedaż i w razie potrzeby podjąć aktywne działania marketingowe w celu jej aktywizacji. Wzrost kosztów marketingu będzie miał niewielki wpływ na wartość NPV, natomiast może istotnie przyczynić się do zwiększenia wpływów ze sprzedaży.

Analiza powyższego projektu rozwojowego firmy transportowej wykazała, że dla wszystkich wariantów projekt jest opłacalny. NPV w każdym przypadku było większe od zera. Analiza ta pozwoliła także wskazać wariant najbardziej opłacalny dla inwestorów. Biorąc pod uwagę wyniki tej analizy można było uznać, że projekt należy realizować, ponieważ w każdym wariancie gwarantował on uzyskanie satysfakcjonującej stopy zwrotu. Jednak zastosowanie metod uwzględniania ryzyka w rachunku opłacalności inwestycji pozwoliło na uzyskanie pełnego obrazu sytuacji. Już analiza scenariuszy i obliczone na jej podstawie odchylenie standardowe NPV zwróciły uwagę na dość wysoki poziom ryzyka, towarzyszącego danej inwestycji. Dzięki zastosowaniu kryterium decyzyjnego, jakim jest współczynnik zmienności można było wskazać wariant charakteryzujący się jednocześnie najwyższą opłacalnością i najmniejszym ryzykiem. Chcąc dokładniej poznać ryzyko towarzyszące danemu wariantowi przeprowadzono analizę symulacyjną i określono prawdopodobieństwo zaistnienia sytuacji, że NPV będzie mniejsze od zera, co wykluczałoby realizację danego projektu. Prawdopodobieństwo to zostało określone na poziomie 40%. W artykule nie próbowano ocenić, czy dany poziom ryzyka powinien wykluczyć realizację danego projektu. Wskazano jednak potrzebę pogłębionej analizy wrażliwości, która pokaże elementy, na które najbardziej narażona jest wartość NPV i które należałoby szczególnie monitorować w przypadku podjęcia decyzji o realizacji inwestycji.

Przedstawione obliczenia i analizy dały pełny obraz sytuacji z punktu widzenia opłacalności inwestycji, a także ryzyka inwestowania. Obliczono efektywność projektu, uwzględniono także ryzyko wykorzystując różne metody. Mimo, że ryzyko towarzyszące projektowi nie jest niskie, przedstawione analizy nie wykluczają realizacji danego projektu. Wszystko zależy od skłonności inwestorów do ryzyka. Dzięki zastosowaniu wielu metod i przeprowadzeniu kompleksowych analiz mają oni większą wiedzę na temat projektu, co powinno być pomocne przy podejmowaniu decyzji inwestycyjnych.